《Flow matching for generative modeling》2023

  对于图像生成，希望让模型学习数据的分布，但很难表示出一个适合采样的复杂分布。

  我们会把学习一个分布的问题转换成学习一个简单好采样的分布到复杂分布的映射。一般这个简单分布都是标准正态分布。

  此时问题便转化为学习映射。

  近年来包括扩散模型在内的几类生成模型用一种巧妙的方法来学习这种映射：从纯噪声（标准正态分布里的数据）到真实数据的映射很难表示，但从真实数据到纯噪声的逆映射很容易表示。

  先人工定义从图像数据集data到噪声noise的变换路线(加噪)，再让模型学习逆路线。让噪声数据沿着逆路线走，就实现了图像生成。

Flow-matching 学习路径

  ODE -> flow -> normalizing flow -> continuous normalizing flow(CNF) -> flow matching -> rectified flow

基础概念

  在本文中，首先需要了解的概念及其彼此关系，流，向量场，概率密度路径。

  注意点: 本篇文章中，是样本，是噪声。

向量场v

  向量场, 定义了一个速度场来表示从起始点到目标点的传送过程，从而产生轨迹。

  简单理解为速度与位置(路程) ，负号是因为定义的的，而推导时做的是采样，故是从(1->0),

流flow

  流，在此处的理解是映射，是运动的轨迹。

但也有别的理解认为，不同的初始会在流的作用下产生不同的轨迹。描述的轨迹，则是ODE的一个个解；描述的每次变化，则是flow。

  为了后文的统一描述，此处认为轨迹，就是要学习的映射。

场与流的关系

  向量场，轨迹

  用向量场构建随时间变化的映射，ODE形式，求解轨迹：   一般用神经网络逼近学习

概率密度路径Pt与流、场的关系

概率密度路径，是和有关，故，。 【积分p从0到1的值是1】

连续性方程：检验向量场是否能产生能从起始点到终止点的概率密度路径，若要产生，需满足偏微分方程(充要)： 其中，，发散算子

[!NOTE]

推导连续性方程：SDE与FPK公式

SDE(随机微分方程)标准形式：，是时间，是漂移系数，是扩散系数，是维纳过程，解是描述的是一个随机过程。

  • 维纳过程：正态，独立增量 ,

​ 重参数化，，，相当于是一个高斯噪声项

既然是随机过程，就有其对应的概率密度，而Fokker-Planck(FPK)就是用于得到（去掉噪声项）： 是拉普拉斯算子对，等价于是求梯度的对 根据已知的FPK公式，推导连续性方程(div搞一起，提取)：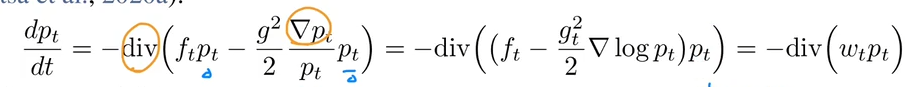

连续性方程推导

对比一下就知道，向量场其实就是

连续归一化流CNF

连续归一化流CNF：用于将一个简单的分布(如纯噪声)，重塑为一个复杂的分布，通过一个前推算子： 其中，是一个前推算子（或称为变量变换）。

前推算子

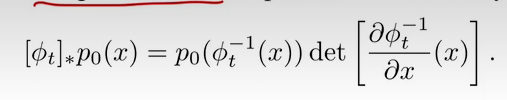
det是雅可比行列式：

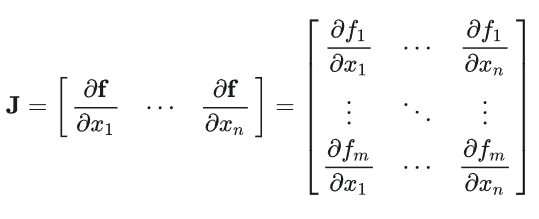
雅可比行列式

CNF理解：可以看作是一个个函数的复合，如x->h1->h2->..->z，经过了,得到，那么CNF就是这么一个复合函数。

变量变换理解：经过，对应分布是和，对两个分布做积分显然有，于是得到，那如果是多维的: ，概率密度大于，取绝对值 根据流的ODE形式： 得,代入式子，就能知道前推算子的来源了。 总结：

  • 场，流，ODE形式串联；

  • 概率密度，前推算子串联(利用)，简单分布到复杂分布；

  • 场与概率密度，连续性方程串联(检验向量场是否能产生概率密度路径)

流匹配FM的目标

原始目标

符号定义：

  • ，样本数据，真实分布未知；
  • 概率路径，设置是一个简单分布。

目标：

  找到一条概率路径，使得能从到，且希望的分布尽可能接近真实分布

形式化表示：

  若已知,，及其对应的真实向量场，则用神经网络拟合。(只要知道场，就能知道流，概率密度)   其中，，表示从采样的所有点的平均误差，FM是Flow Matching（流匹配）的缩写。

  • 内层积分：对时间 t 的某一固定值，求从 中采样的 上的误差。

  • 外层积分：对所有时间点 的误差平均化

面临问题：但这个假设和已知是很困难的，所以后面会用条件概率密度来替换。

此时，已经知道了目标，那么为了能够继续优化，显然是对的形式作各种处理。

构造目标路径p_t(x)

采用简单的概率路径来构建目标概率路径：

是样本数据，是条件概率路径，且满足:

  • 在时，是一个简单分布；(与无关)

  • 在时，要如何才能接近真实分布？

    文中设定的是类似一个脉冲的形式：,是很小的正数。

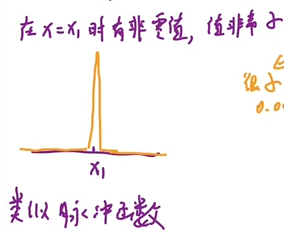
高斯脉冲函数

将条件概率路径进行边缘化，关注，消除变量，正常边缘化的公式是，此处做了近似： 性质：

  • (因为概率密度积分值为1)；
  • ，

为什么可以近似？脉冲函数的理解

设置t=1时是高斯函数(脉冲函数/卷积)，形式是类似狄拉克函数(x=0处值为＋∞，其他处为0)，好处是筛选性。

对于一个分布，混合一个狄拉克函数： 推导方式，因为只有当时这个积分才有值，所以用替代，积分值是1。

可写作卷积，这种f和g的联合概率分布，也称为卷积形式。

回到，根据高斯分布函数的定义： 所以，把它理解为是一个关于的函数(与高斯分布函数f不一样)

故，即卷积

构造向量场u_t(x)

给定能产生条件概率路径，则它们满足连续性方程： 其中，，发散算子 对于真实分布，可进行边缘化得到，要得到的形式，从连续性方程入手：

与需要满足连续性： 目标 证明，对，两边对t求导，再代入连续性方程，交换积分(对x_1)和求导(对x)，独立的不影响，得： 此时，要得到目标，故对乘一个,除一个，即，对比，可以得到:

条件流匹配CFM

先前存在问题：由于前面构造的和是积分形式，不容易进行计算，从而导致原目标不好计算。

解决方法：更简单的目标，且能产生与原目标相同的最优结果。

假定已知，那么就可以从中采样，并计算，从而避免去计算积分。 其中，，是目标真实分布。

  • 如何保证与原目标相同的最优结果？

神经网络的参数，是梯度值计算，需保证梯度值一样。 证明如下：

证明：

假设：

  • 为保证积分的存在性，需允许交换积分次序；
  • 和在时趋于0；
  • 有界。

对于两个目标， 外面都是算期望，先不管，取出里面的二范数并做展开，中间项是内积： 由于只考虑神经网络的，故可把最后一项划掉。

若能保证两项的结果是一样的，那么就说明等价了。

先考虑，与的等价性，展开为积分，然后利用被推出来的边缘化公式： 再考虑，与的等价性，展开为积分，代入的形式，然后可以约掉(因为内积具有线性性质，)，然后交换积分和内积的顺序(先内积再积分，可提x1)：

条件概率路径与条件向量场

为了让条件更加简化，假定条件概率路径是高斯建模: 其中，，(大于0就行，因为是一个标量乘单位阵)，是样本数据

设定

  • t=0，; 标准高斯分布
  • t=1，， 以为中心的高斯分布

为什么是高斯

大部分向量场会产生额外计算(?)，而高斯的话能产生符合条件且最简单的向量场。

（概率路径 -> 流(轨迹)）进行参数化，仿射变换： 其中，是从标准高斯分布采样得来。

概率路径的迭代方式：

根据，故假定已知，那么就能知道，且有(是标准高斯)： 条件流与条件场

原先的流与场：

条件流与场：

代入CFM目标函数：，得到： 条件概率路径->条件场

假定已知是一个高斯概率路径，根据的仿射变换，以及条件流与场的关系，于是就能给出定义的向量场： 结果，能产生高斯路径,从而知道的形式。

证明：(利用了流与向量场的关系进行变量替换，然后利用条件概率路径对应的进行代入高斯假定)

令，则等价于.

通用变量替换：令则，于是有

代入特定高斯假定：

  • 根据，得
  • 根据，两边对t求导，得

代入，得：

高斯条件概率路径的特例

验证条件概率路径推出的条件向量场能成立，以下给出两个特例：(但以下只讲扩散模型相关的特例)扩散模型相关的条件VFs和最优传输

扩散模型相关的条件VFs

前置知识:

扩散模型的两个类型: Variance Exploding(VE)和Variance Preserving(VP)

VE和VP是来自Score-based那篇文章(通过SDE的基于分数的生成建模)

要注意本文和那篇文章的符号不一样。

VE: 方差爆炸(SMLD)

朗之万动力学，有点类似梯度下降+随机项

一般的扩散模型流程：

扩散流程

(1)单步加噪：，其中，方差是提前设定的。

VE中要求是递增的: ，一般是一个等比数列

(2)离散马尔科夫：

当前状态依赖上一步状态， （直接加噪声项）

(3)方差爆炸性：

随着时间增加，方差增大

由来：单步加噪分布() -> 离散马尔可夫 -> 连续化，SDE形式，求解 -> 求解方法，求期望和方差。

主要针对方差，即，在VE中，是递增的，所以方差也会一直递增。

VP: 方差保持(DDPM)

(1)单步加噪：，其中，是事先设定的。

VP中要求，0~1之间即可，不用递增，

一般是线性插值，给定和就行，

(2)离散马尔可夫：

（原图处理，再加噪声）

这么设置的原因：希望最终噪声图是,那么令，

由DDPM的一步加噪，可得最终噪声图，且随着增加，

于是最终结果就会趋近。

(3)方差不变性

随着时间增加，方差有上界。

的处理，是，其中，，

高斯条件概率路径 ，可通过SDE形式推导：

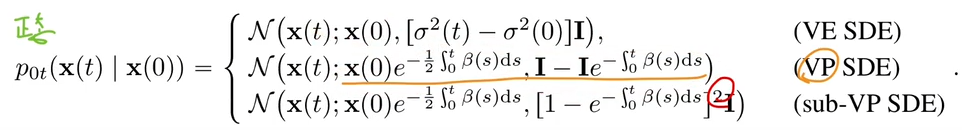
SDE形式P_t

由条件概率路径(Score-based) -> 条件向量场：

已知,(此处符号不太一样，原图样本[t=1]是,噪声图[t=0]是，于是令t=1-t，之前符号的视作）

推导思路一：CFM指导

VE的向量场推导

此处，因为原样本已给出，不存在方差一说，故是0。

勘误：不是去噪，都是加噪的(data->noise)

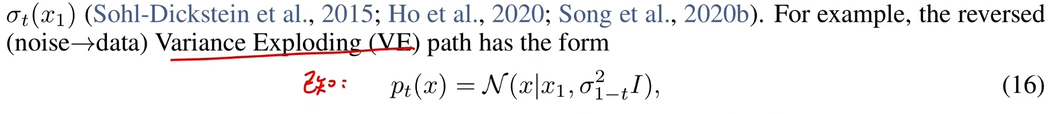
VE的P_t

由,其中‘是关于t求导。

所以得到：

VP的向量场推导

勘误：不是去噪，都是加噪的(data->noise)

VP_Pt

同理得到：

  • 为什么选择流匹配(计算这个场)，分数模型不行吗？

(1)实验证明，结果更稳定，鲁棒

(2)之前SDE求解得到的理论解，不一定能在有限时间内得到这种噪声分布，是一种理想解；

但是在流匹配中，只需要设置和，那么就可以控制概率路径。

推导思路二：SDE与FPK

之前讲的那种，是通过，然后给定和来代入公式，求得向量场。

另一种思路，通过SDE的形式，经过FPK公式，得到概率路径，再得到向量场。

符号定义

扩散模型中是数据(t=0) -> 噪声(t=1)，而在流匹配中是数据(t=1) -> 噪声(t=0)

于是得到的定义是：，

为什么加了负号？

由连续性方程：，而此时：

SDE得到向量场(前面推导的)：

推导连续性方程：SDE与FPK公式

SDE(随机微分方程)标准形式：，是时间，是漂移系数，是扩散系数，是维纳过程，解是描述的是一个随机过程。

  • 维纳过程：正态，独立增量 ,

​ 重参数化，，，相当于是一个高斯噪声项

既然是随机过程，就有其对应的概率密度，而Fokker-Planck(FPK)就是用于得到（去掉噪声项）： 是拉普拉斯算子对，等价于是求梯度的对 根据已知的FPK公式，推导连续性方程(div搞一起，提取)：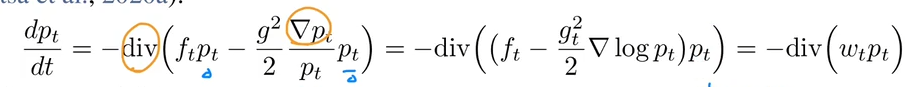

连续性方程推导

对比一下就知道，向量场其实就是

如果要求这个向量场，只要把得到(对y求导)。

VE向量场推导

SDE标准形式是，

VE的SDE形式(score-based推导的)，： 对于：

首先，概率路径就是：

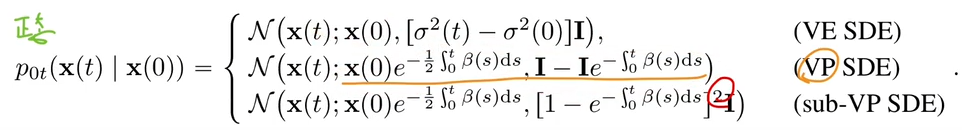
SDE形式P_t

，把它写成高斯函数的形式：

高斯函数

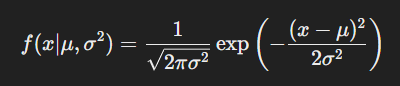
即 代入，得： 然后再把下标变一下(之前都是t=0->1)，现在是1->0： VP向量场推导

SDE标准形式是，

VP的SDE形式(score-based推导的)，，，： 概率路径

同理求

结果得到： 求出来的w和前面的u是一样的。

Flow Matching总结

注意点，本篇文章中，是样本，是噪声。

  1. 流，场，概率密度，彼此关系

    流与场 原文公式(1)(2) 概率密度与场 原文公式(26) 其中，，发散算子 简单分布推， 原文公式(3)(4)

  2. 流匹配目标

找到一条概率路径，能从得到

研究对象是场，知道了场同样就知道概率路径。

实现：神经网络拟合向量场，那么就需要知道这个场的表示形式。

  1. 如何表示（3个定理)

定理1： 证明/给出的形式 (如果知道了也不用拟合了，显然难以计算得知)

定理2： 由于前面给出的形式有积分不容易计算，故替换为加了条件的形式

​ 能否替换？ 需证明原目标损失的梯度和现目标损失的梯度一致

定理3： 把条件更简化，高斯条件下的向量场

​ 验证：(1)用扩散过程的VE和VP (2)最优传输(此处没讲)

​ 其中VE和VP的验证分为两个思路：(1)直接用定理3推VE和VP的条件向量场； (2)SDE+FPK公式推导条件向量场

参考

2.1介绍流Flow的定义和作用，理解向量场vt和ODE_哔哩哔哩_bilibili