论文阅读-统一视角理解扩散模型
Understanding Diffusion Models: A Unified Perspective
《Understanding Diffusion Models: A Unified Perspective》
【论文精读】Understanding Diffusion Models: A Unified Perspective 01【introduction】_哔哩哔哩_bilibili
Instruction: Generative Models
生成模型定义
作用:
任意生成一个新样本
评估观测或采样数据的似然性
现有生成模型
(1)Generative Adversarial Networks (GANs)
通过对抗的方式,在复杂的分布中进行采样。
(2)likelihood-based
基于似然值,使得观测样本的似然值越大越好。
autoregressive models 自回归
normalizing flows 归一流
Variational Autoencoders(VAEs) 变分自动编码器
(3)energy-based
能量函数建模,将要学习的分布转为能量函数。
(4)Score-based
能够用能量函数的分数作为神经网络学习的评判准则。
本文工作,通过基于似然的角度和基于分数的角度,解释扩散模型。
Background: ELBO, VAE, and Hierarchical VAE
在生成建模中,通常寻找低维的潜在特征学习,而不是高维特征。
原因:
如果要学高维特征,需要有强大先验。
对于低维,可以视作信息的压缩,更有可能能找到能表示观测数据的有意义的结构。
Evidence Lower Bound(ELBO)
(1)
的一个下界 (2)为什么就选ELBO作为下界
将潜变量和观测样本放在一起建模:
似然函数的目标:对于观测的
此时,如何从
边缘化
(1) 条件概率
,(2),理解: 的发生,是先发生 然后在 的基础上再发生事件
直接计算(1)式,涉及积分,计算复杂;
直接计算(2)式,涉及真实编码器
于是根据这两个式子,衍生出了Evidence Lower Bound (ELBO)
Evidence: 此处表示的是观测数据的对数似然
目标是
存在的问题:如何得到
采用条件概率法,就需要去近似这个真实的后验分布
,也就是训练一个encoder:
在原文中,将目标转化为了去最大化这个对数似然的下界,即代理目标:
为什么要选择
ELBO?证明目标:
推导过程:

数学期望的知识:
随机变量:
, 离散化:
是 的分布函数, , Jensen’s inequality(杰森不等式):
要求
是凸函数,即开口朝上的函数。 而此处的log x是凹函数,于是把≤变成≥: 如何说明在那么多下界中,就是要选择 ELBO?
期望的分离:
KL散度:用于度量两个分布的接近程度,越接近,KL散度越小,一定是大于0的,最好是趋近于0
其中,
是近似变分分布, 是真实后验分布
此时,回到我们的目标:
- 对数似然
尽可能大 尽可能近似真实分布
直接计算KL散度是困难的,因为不知道
在给定数据
所以,优化目标变为了最大化ELBO。
选择ELBO作为下界:
既能保证编码分布与真实后验分布足够接近
一旦训练后,可以用来观测生成数据的似然性,因为
其实很大部分取决于ELBO,DL散度很小的。
Variational Autoencoders
Diederik P Kingma and Max Welling. Auto-encoding variational bayes. arXiv preprint arXiv:1312.6114, 2013.
变分自动编码器
在VAE的默认公式中,都是直接最大化ELBO。
variational:寻找最优的潜在后验分布
autoencoders:输入和输出是同一个维度上的值
具体来说,

链式法则:
期望的分离:
解释:
第一项是通过
来重建 ,是 decoder部分,称为重构项;第二项是通过
去近似先验 ,训练 encoder,称为先验匹配项,这里的理解可以是图像的颜色之类的先验信息,此处是在度量学习到的后验分布能保留多少的先验信息,可以理解为控制出图先验要求。 目标:
如何来优化求解未知参数
为计算和优化方便,VAE的encoder一般选择对角线协方差的多元高斯分布,先验选择标准多元高斯:
在假定高斯了之后,
- 蒙特卡罗(
Monte Carlo)近似
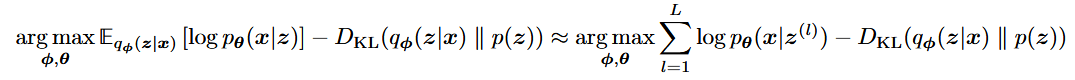
对于
然后对所有样本点作平均
在此处,潜变量
存在的问题:因为是随机取值,那么在算loss的时候就通常是不可微分的,就没办法求梯度,不能采用梯度下降算法去优化。这种随机变量的选择会导致损失函数的值在样本之间发生跳跃,从而使得损失函数变得不连续。
- 重参数化(
reparameterization)
可以将随机变量重写为噪声变量的确定性函数,如
在VAE中的做法是,将
Hierarchical Variational Autoencoders
VAE的推广,分层变分自动编码器HVAE,推广点:
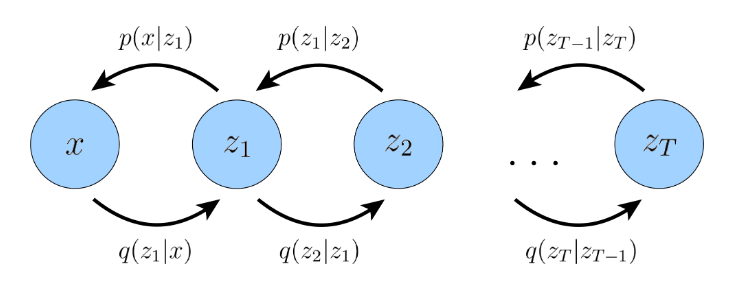
在每个隐变量由之前的隐变量为条件产生的情况下,我们关注一种叫做马尔可夫HVAE(Markovian HVAE (MHVAE))的情况。
Markov chain: 马尔科夫链
马尔可夫性质:当前时刻的变量只对于前面的一个时刻的变量具备依赖性。
此时的优化目标,仍然是最大化ELBO,但推导方式有点不同。
[!NOTE]
正常情况下,条件概率公式:
马尔可夫性质(只与前一个有关),联合分布(解码)和近似后验分布 (编码): ELBO的积分推导:

于是根据马尔可夫性质,代入可得:
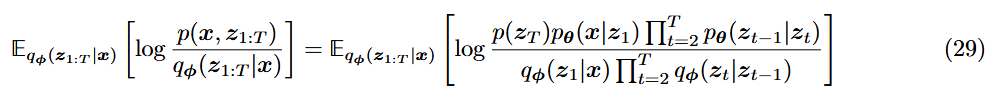
(29)式,在变分扩散模型(VDM)中会进一步进行拆解。
Variational Diffusion Models
three key restrictions & 扩散流程
VDM,可以视作是一个特殊的MHVAE,带有三个限制(a Markovian Hierarchical Variational Autoencoder with three key restrictions):
潜变量
维度与数据 维度一致 每一步的潜变量编码器是线性高斯模型(简单),且只依赖上一个时间步的结果(马尔可夫性质)
具体而言就是,每次
是在建模一个高斯分布,其将前一步的状态作为它的均值。 最后的潜变量分布经过一次次编码后,得变成是标准高斯分布(加噪)
详细介绍三个限制:
[!NOTE]
(1)针对第一个限制:符号替换
符号定义:
代表的是true data samples
代表的是潜变量 ,所以encoder由原来的 可以写作: (2)针对第二个限制: 他每个时间步的encoder结构是可以学习,或预设为高斯的超参数。
每一步的mean是依赖上一步,而方差variance是保留的(variance-preserving)
编码过程encoder:
给定 ,该过程是一个确定的过程。 (3)针对第三个限制
decoder部分,首先是
是一个标准高斯分布,然后从右往左去噪。
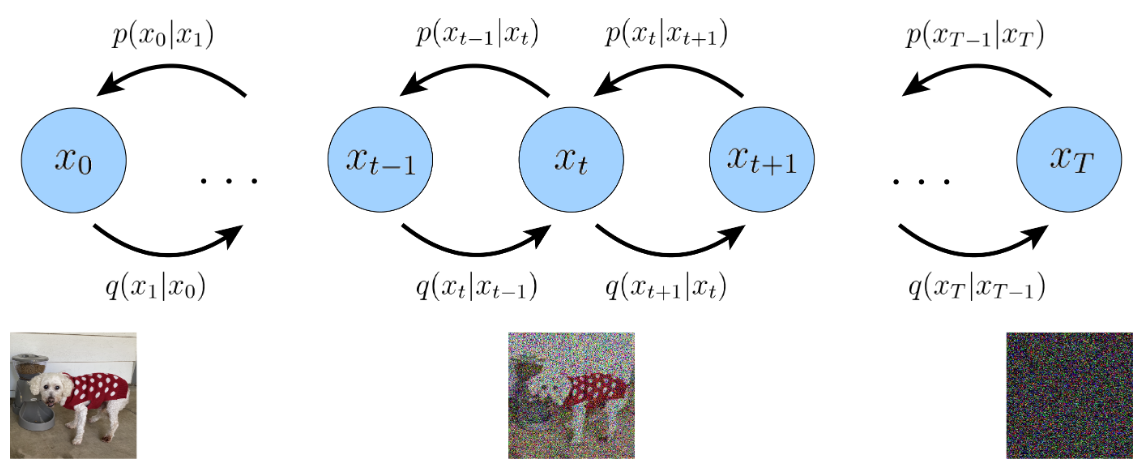
加噪:每步逐渐添加噪声破坏原图像,直至变成一个纯噪图
encoder无需
,因为是被视作每个时间步的高斯建模,参数是可以预设给定的。 去噪:
decoder才是唯一感兴趣的部分,
,需要训练。
在训练模型完毕后,采样流程:
首先,从
优化目标ELBO:第一种拆解方式
VDM的优化目标,最大化ELBO:
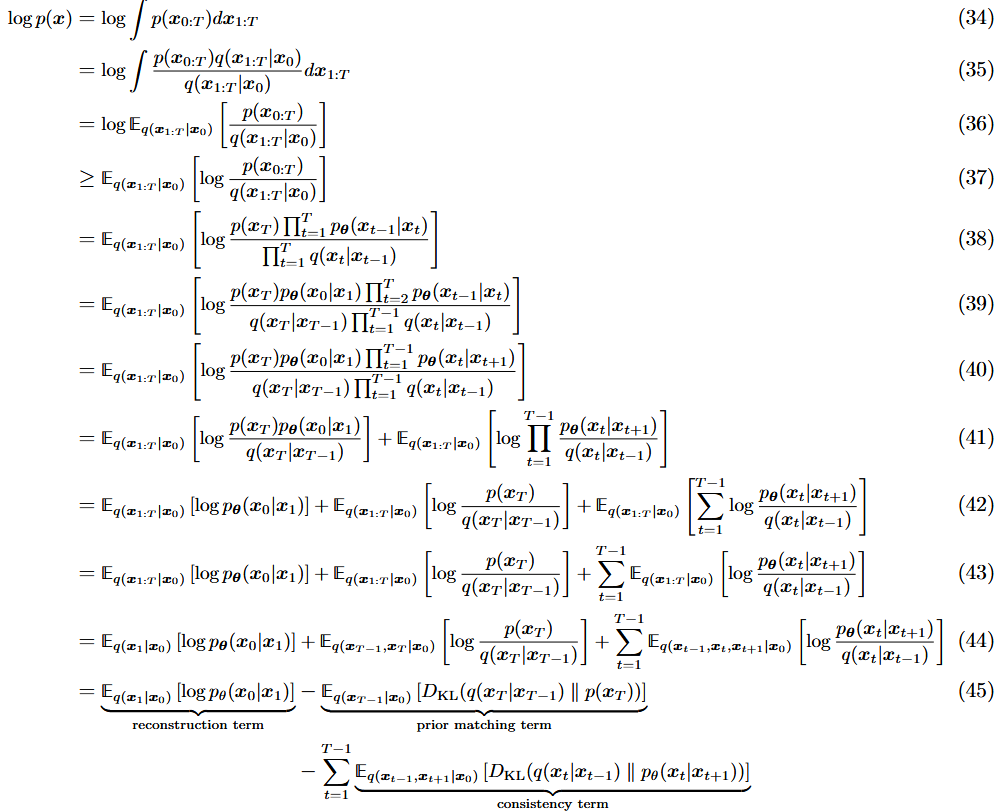
此处的
重构项(reconstruction term):重建效果,给定加噪分布,去噪后尽可能接近原始图像,用log似然值来度量,越大越好。
先验匹配项(prior matching term):先验匹配,加噪的最后一步尽可能接近标准正态,KL散度度量接近程度,越小越好。【无需训练,无训练参数,当T足够大,可视为0】
一致性项(consistency term):对于每步,
不管是向前加噪和向后去噪,都保持一致,求和是对每一步都要来计算匹配程度,越小越好。(耗时最多)
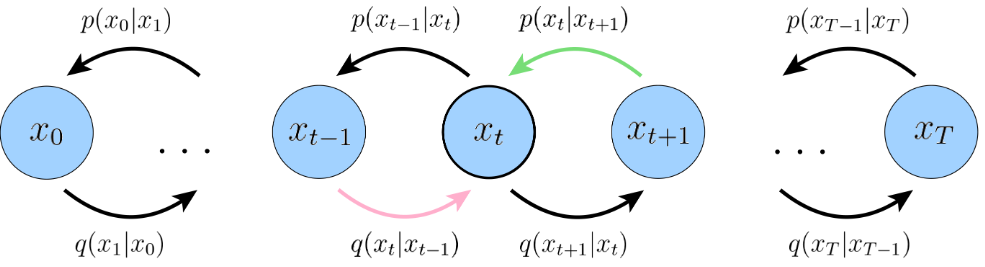
优化目标主要由第三项主导,故需要对每步时间t进行优化。
优化目标ELBO:第二种拆解方式
第一种拆解ELBO方法的特点:
1.前面对ELBO的拆分成三项,且都出现了期望,那么就可以用蒙特卡洛的方法,从分布中抽样,然后代入多次,求平均值近似计算。
2.但是,ELBO的第三项涉及到两个变量
,会导致估计出来的方差比单个变量估计的方差还要大。 原因:扩散过程的加噪和去噪,都从标准正态中采样噪声,对于
,需采样两次。由于采样次数增加,累积随机性的影响会导致更大的波动,即更大的方差。 3.随着T增大,一致性项估计的方差也会增大。(因为有T-1次方差计算)
第二种拆解ELBO的方式:旨在尽可能缓解第三项存在的问题。
目标:推导出的每一项,就只与一个随机变量有关。
拆解方式如下:

推导如第一种的(38)式 (48);分子提t=1,分母也提t=1 (49);对
约分,(53)(54):
期望性质,(56);
每项涉及相关的变量,分布里才体现,因为是独立的,故可直接去掉,(57);
第一项不变,第二项KL散度,第三项二重积分
重构项(reconstruction term):重建效果,给定加噪分布,去噪后尽可能接近原始图像,用log似然值来度量,越大越好。 (和上面一样)
先验匹配项(prior matching term):与第一种推导的:
含义是一样的,只是形式不一样。 先验匹配,加噪最终生成的噪声尽可能接近标准正态,KL散度度量接近程度,越小越好。【无需训练,无训练参数,当T足够大,可视为0】
去噪匹配项(denoising mathcing term):与第一种推导的
,要看前后两项存在区别,此处只需要看去噪。
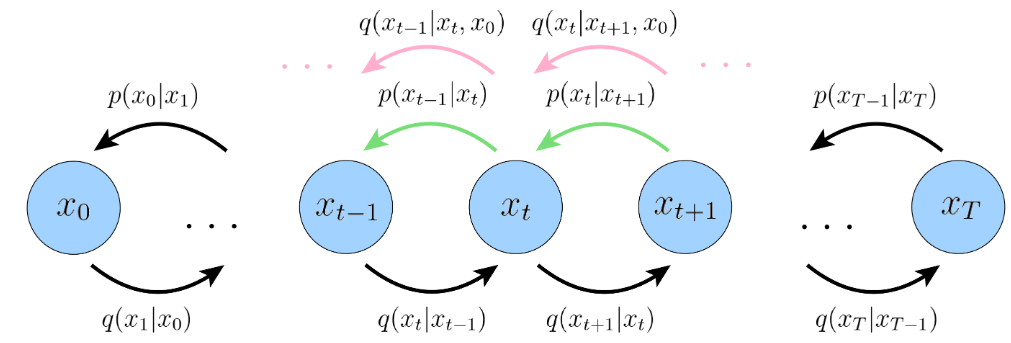
真实去噪分布
近似去噪分布
此时只涉及一个随机变量
ELBO的简化:引入高斯限制
主要优化重点在于去噪匹配项。
- 加噪过程引入高斯限制
由VDM是一种带有三个限制的MHVAE,其第二个限制中提到:
encoder过程(加噪过程)是一个固定的高斯模型
而为了能够利用上梯度下降法,需要对其进行重参数化(可以直接从0->t):
[!NOTE]
加噪过程的确定性公式:
,给定 和 ,可直接给出 ELBO的优化成本,重点在于求和项即去噪匹配项(真实去噪分布||近似去噪分布)
已知加噪过程的
,可写作: 就是不断的往回带,且每次的正态分布是独立同分布的,故两个正态分布相加后,仍然是正态分布(63)->(64)。
, , 与 独立,则 ,均值和,方差和。 在式子中,就是
和 两个分布合起来。 令
。
此时已知高斯限制的加噪过程,如何去表示去噪匹配项中的真实去噪分布
- 表示真实去噪分布
去噪的时候(解码器),通过贝叶斯公式来转换式子,以加噪来推出去噪分布:
最终结果仍为高斯:
去噪,给定
和 ,来反推 
首先通过贝叶斯,将去噪式子转换为已知的加噪,然后代入式子:累加项
,递推项 (71)(72); 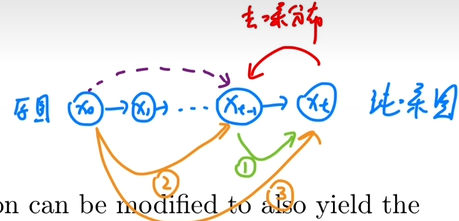
对于(73),如
,代入高斯函数 ,不看系数项,就可得到;(这里面涉及到多维高斯的理解, ,单独看 是上面这个式子,然后由于每个 之间是独立的,此处是相当于对每个 都做了这么一个函数的操作,是逐元素的) 对于(75),只关心与
有关的项,将(74)的前两项平方项展开,然后与 有关的放一起,其他就放到后面常数部分 中(相当于 ,此项视为常数)。 (76)~(80),整理通分,
样子 (81)~(83),凑成高斯函数的样子,
, 是常数,与 无关,所以可以忽略。
对于
和 的形式推导如上,其中 可以预设
,或者去学习; 令
,
由于
其中,方差是已知的。
由于真实去噪分布
其中,令
- 两个高斯分布的KL散度
$$
其实就是两个分布的均值差距了。对于近似去噪分布,各种优化的不同设定,都是围绕
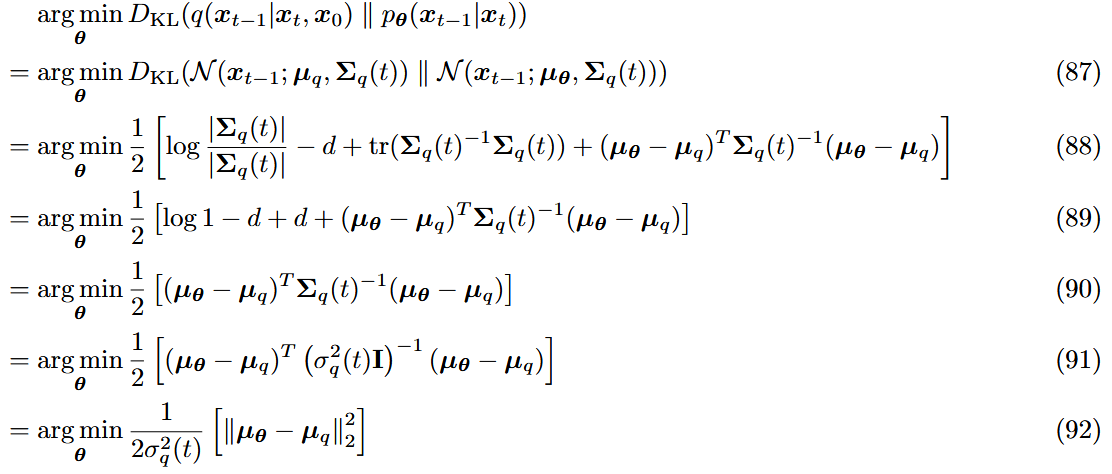
两个高斯分布之间的KL散度计算:
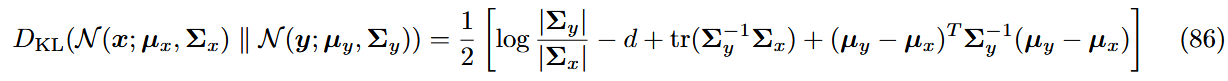
在
和 中, 设置为一致; 的意思是 ,单位阵的迹是对角线元素的个数,若维度为 ,加起来就是 ; 由于
,
- 设定1
已知
此时转化为了
输入:噪图
输出:原图
目标:
对于ELBO中的第三项,去噪匹配项
扩散模型第一步,都是任意取时间步
优化目标的Three Equivalent Interpretations
论文标题,统一视角看待扩散模型,指的就是三种优化目标的等价性。
扩散模型的优化目标:ELBO的第三项(真实去噪分布和近似去噪分布的匹配),在高斯限制下(MHVAE+限制)的转换如下:
优化目标的等价来源:对
已知(高斯限制下):
(1)一步加噪是确定性过程:
(2)真实去噪分布:
思路
根据
(1)设定1:预测原图
(2)设定2:预测噪声 (DDPM采样器)
首先,对于一步加噪
然后,代入
预测噪声和预测原图的等价性:
,由这个式子, 和 的关系是固定的(因为有常数,输入 )。 所以预测
和预测 是等价的。 但有的文献说预测噪声效果更好,因为预测原图的话要塑造很多次,而噪声可能误差更小
(3)设定3:Score-based
通过Tweedie公式,可以得到
Tweedie公式推导:使用条件: 指数分布族(常用于正态)
作用: 给定样本下,计算后验均值的估计
给定样本
,根据 Tweedie有:证明:
设
是先验分布, 是样本分布/密度 ,给定 ,估计 的值 后面的推导较为复杂,最后求出来的结果是 , 是 的似然函数(样本分布的边缘化) 。
应用于扩散过程已知一步加噪
,根据 Tweedie,于是有。 又
,所以有:
在设定1的基础上,将
分数函数
(1)预测梯度和预测原图的等价性:
, ,所以可以知道,预测原图 ,预测噪声 ,预测梯度 ,三者都是等价的,关系是固定的。 (2)联立上面两个式子,可以知道:
,似然函数的梯度更新方向,是初始噪声的负方向。
Learning Diffusion Noise Parameters
对于超参数
于是此处采用推导的方式,能够高效地求解
通过设定1的设置,学习原图的优化目标:
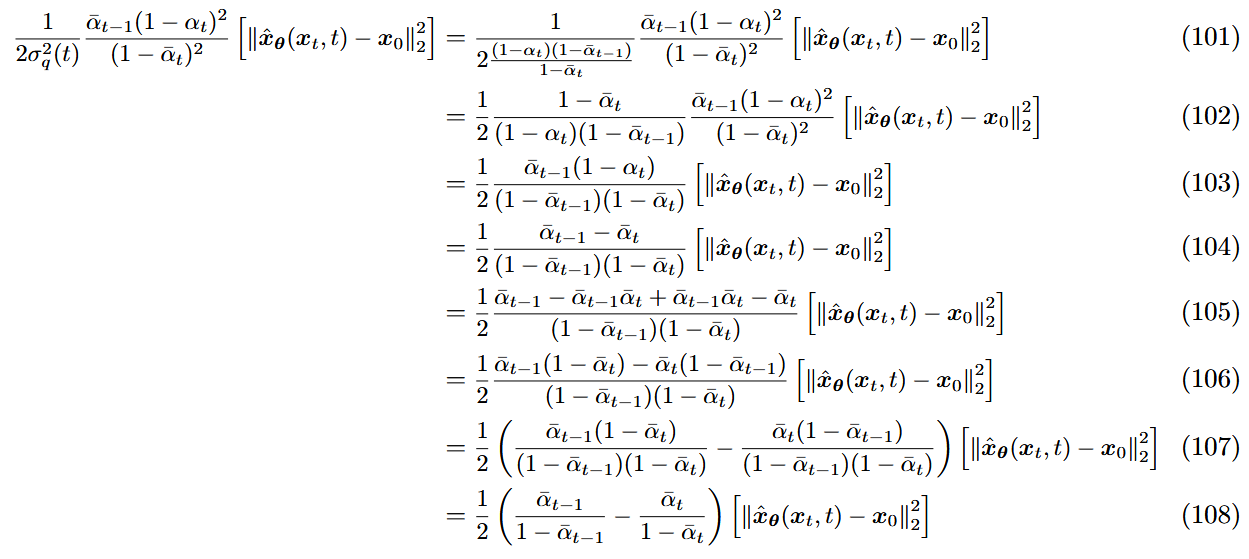
接下来,对于
在优化目标时,还会再学习一个递增的神经网络
具体推导过程:
信噪比signal-to-noise ratio(SNR)此处取的是完全确定的加噪过程:
,将每个时间步的信噪比设定为: 原优化目标就可简化为: 信噪比可以理解为 ,越高,说明原信号信息越多(原图清晰点多);越小,说明噪声越多。 原 信 号 噪 声 量 在扩散模型中,加噪过程,SNR随着t增大而减小,直到
,达到标准高斯噪声。 根据这个性质,于是给出
的新设定:单调递减函数 其中, 是单调递增的。此处用神经网络实现,但如何保证单调递增的神经网络? 假设是线性网络Y=WX,此时只要保证W是正的就能单调增,一个简单的办法为设计W=w1*w1,同样的参数乘两次;假设是非线性网络Y=A(WX),A为非线性激活函数,此时可采用单调增的非线性激活函数(例如leakyrelu,sigmoid),结合上者应当也是单调增;此外归一化层作为缩放,应不改变单调性;将三者叠加应该可做到拟合单调增的任意函数。
联立
的两个式子,可以得到: 所以 令 ,
Guidance
为扩散模型添加条件控制(学习条件分布)
正常去噪过程的联合分布:
每个时间步引入条件信息:
优化目标,有三种(预测原图,噪声,分数模型),主要是在优化第三项:
分别引入条件信息:
这种直接引入一个条件信息y的做法,导致的问题是控制力度不够强(容易被忽略或淡化),解决方法是对条件信息赋权,加强条件控制,以下给出了两种方法:
Classifier Guidance
第三类优化目标,分数函数学习
利用贝叶斯,进行拆解,此处的

是对
unconditional score: 无条件分数扩散模型
adversarial gradient:
对抗梯度。噪声分类器的对抗梯度,这个噪声分类器是接收输入
为了能控制条件的力度,引入超参数
Classifier-Free Guidance
在
利用贝叶斯改进这个对抗梯度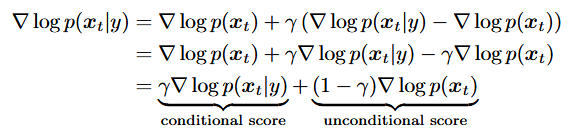
在实际训练过程中,单独训练两个模型代价昂贵,所以会把条件扩散模型和无条件扩散模型一起训练:
只训练一个条件扩散模型